hot100链表2题解

发表于 2025/01/16 更新于 2025/01/16

作者 匆匆那年 42 分钟阅读

19. 删除链表的倒数第 N 个结点

问题描述

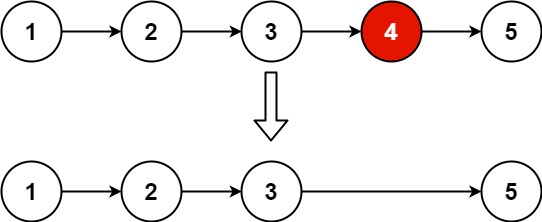
给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

输入：head = [1], n = 1
输出：[]

示例 3：

输入：head = [1,2], n = 1
输出：[1]

提示：

链表中结点的数目为 sz
1 <= sz <= 30
0 <= Node.val <= 100
1 <= n <= sz

进阶：你能尝试使用一趟扫描实现吗？

题解

解题思路

为了删除链表的倒数第 $n$ 个节点，有两种常见的方法：

两次遍历：
- 第一次遍历计算链表的长度。
- 第二次遍历找到倒数第 $n$ 个节点的前一个节点，并删除目标节点。
一次遍历（双指针法）：
- 使用快慢指针：
  - 快指针先走 $n+1$ 步，慢指针从头开始。
  - 然后快慢指针同时移动，直到快指针到达链表末尾。
- 此时慢指针正好指向倒数第 $n$ 个节点的前一个节点，删除即可。

方法 1：两次遍历

C++ 实现

  
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */

class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        // 计算链表长度
        int length = 0;
        ListNode* temp = head;
        while (temp) {
            length++;
            temp = temp->next;
        }

        // 如果删除的是头节点
        if (n == length) {
            return head->next;
        }

        // 找到待删除节点的前一个节点
        temp = head;
        for (int i = 1; i < length - n; i++) {
            temp = temp->next;
        }

        // 删除目标节点
        temp->next = temp->next->next;
        return head;
    }
};

方法 2：一次遍历（双指针法）

C++ 实现

  
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode dummy(0); // 哨兵节点
        dummy.next = head;
        ListNode* fast = &dummy;
        ListNode* slow = &dummy;

        // 快指针先走 n+1 步
        for (int i = 0; i <= n; i++) {
            fast = fast->next;
        }

        // 快慢指针同时移动
        while (fast) {
            fast = fast->next;
            slow = slow->next;
        }

        // 删除目标节点
        slow->next = slow->next->next;

        return dummy.next;
    }
};

示例讲解

示例 1

输入：head = [1,2,3,4,5], n = 2 输出：[1,2,3,5]

快指针先走 3 步（n+1=2+1n+1 = 2+1）。
快慢指针同时移动，快指针到达末尾时，慢指针指向值为 3 的节点。
删除值为 4 的节点。

示例 2

输入：head = [1], n = 1 输出：[]

快指针先走 2 步（越过链表）。
快慢指针同时移动，慢指针停留在哨兵节点。
删除值为 1 的节点。

示例 3

输入：head = [1,2], n = 1 输出：[1]

快指针先走 2 步。
快慢指针同时移动，慢指针指向值为 1 的节点。
删除值为 2 的节点。

时间和空间复杂度

方法 1：两次遍历

时间复杂度： $O(L)$，其中 $L$ 是链表的长度。
空间复杂度： $O(1)$。

方法 2：一次遍历

时间复杂度： $O(L)$，只需一次遍历。
空间复杂度： $O(1)$。

推荐方法 2（一次遍历），效率更高，代码更简洁。

24. 两两交换链表中的节点

问题描述

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

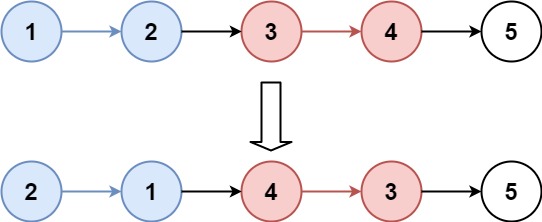
输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：

输入：head = []
输出：[]

示例 3：

输入：head = [1]
输出：[1]

提示：

链表中节点的数目在范围 [0, 100] 内
0 <= Node.val <= 100

题解

解题思路

这道题要求两两交换链表中的相邻节点，需要注意以下几点：

不能修改节点值，需调整节点指针。
递归法： 每次交换一对节点，并递归处理剩余部分。
迭代法： 使用指针逐步遍历链表，调整每一对节点的连接。

以下是递归法和迭代法的实现。

方法 1：递归法

如果链表为空或只有一个节点，直接返回链表头。
对于每一对节点，将第二个节点指向第一个节点，第一个节点指向后续递归处理的结果。
返回第二个节点作为当前子链表的新头。

C++ 实现

  
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */

class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        // 终止条件：链表为空或只有一个节点
        if (!head || !head->next) {
            return head;
        }

        // 保存第二个节点
        ListNode* second = head->next;

        // 递归处理剩余部分
        head->next = swapPairs(second->next);

        // 交换当前两个节点
        second->next = head;

        // 返回新的头节点
        return second;
    }
};

方法 2：迭代法

使用一个哨兵节点 dummy 指向链表头，以便处理头节点的交换。
定义指针 prev 指向每一对节点的前一个位置。
逐步交换每一对节点：
- 将前一个节点的 next 指向第二个节点。
- 调整两个节点的指针指向。
- 更新 prev 指针。
返回哨兵节点的 next 作为结果。

C++ 实现

  
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        ListNode dummy(0); // 哨兵节点
        dummy.next = head;
        ListNode* prev = &dummy; // 前一个节点

        while (prev->next && prev->next->next) {
            ListNode* first = prev->next;
            ListNode* second = first->next;

            // 调整指针
            first->next = second->next;
            second->next = first;
            prev->next = second;

            // 更新 prev 指针
            prev = first;
        }

        return dummy.next;
    }
};

示例讲解

示例 1

输入：head = [1,2,3,4] 输出：[2,1,4,3]

初始链表：1 -> 2 -> 3 -> 4
交换第 1、2 节点：2 -> 1 -> 3 -> 4
交换第 3、4 节点：2 -> 1 -> 4 -> 3

示例 2

输入：head = [] 输出：[]

链表为空，直接返回空。

示例 3

输入：head = [1] 输出：[1]

只有一个节点，无法交换。

时间和空间复杂度

方法 1：递归法

时间复杂度： $O(n)$，每次递归处理两个节点。
空间复杂度： $O(n)$，递归调用栈的深度为链表长度。

方法 2：迭代法

时间复杂度： $O(n)$，每对节点只遍历一次。
空间复杂度： $O(1)$，只使用了常量额外空间。

总结

递归法： 代码简洁，适合递归思维，但存在递归调用栈的开销。
迭代法： 更高效，推荐用于实际应用。

25. K个一组翻转链表

问题描述

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

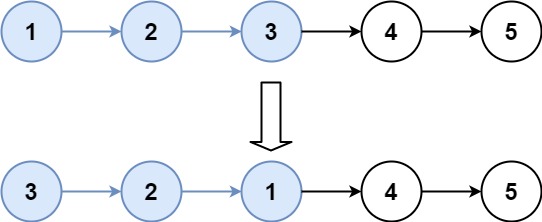
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

提示：

链表中的节点数目为 n
1 <= k <= n <= 5000
0 <= Node.val <= 1000

进阶：你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

题解

解题思路

这道题要求每 kk 个节点一组翻转链表，并且需要满足以下条件：

局部翻转： 每次只翻转 $k$ 个节点，剩余不足 $k$ 的部分保持原样。
指针操作： 不能修改节点值，需要通过调整节点指针来实现。
空间优化： 在 $O(1)$ 额外空间内完成。

实现步骤

统计链表长度： 通过一次遍历计算链表的总长度，判断是否需要翻转。
分组翻转：
- 使用哨兵节点 dummy 方便操作。
- 逐步翻转 $k$ 个节点，翻转完成后将翻转后的子链表连接到前面。
- 更新指针，移动到下一组。
停止条件： 剩余节点不足 $k$ 时，直接保持原顺序。

C++ 代码实现

方法：迭代法

  
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */

class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        if (!head || k == 1) return head;

        ListNode dummy(0); // 哨兵节点
        dummy.next = head;
        ListNode* prevGroup = &dummy; // 上一组的尾节点
        ListNode* end = head;

        while (end) {
            // 找到当前组的结尾节点
            for (int i = 1; i < k && end; i++) {
                end = end->next;
            }

            if (!end) break; // 不足 k 个节点，退出循环

            // 记录下一组的起点
            ListNode* nextGroup = end->next;

            // 翻转当前组
            ListNode* prev = nullptr;
            ListNode* curr = prevGroup->next;
            while (curr != nextGroup) {
                ListNode* tmp = curr->next;
                curr->next = prev;
                prev = curr;
                curr = tmp;
            }

            // 连接前后两组
            ListNode* start = prevGroup->next; // 当前组翻转后的尾节点
            prevGroup->next = end;
            start->next = nextGroup;

            // 移动指针到下一组
            prevGroup = start;
            end = nextGroup;
        }

        return dummy.next;
    }
};

示例讲解

示例 1

输入：head = [1,2,3,4,5], k = 2 输出：[2,1,4,3,5]

分组：
- 第一组：[1,2] → 翻转为 [2,1]。
- 第二组：[3,4] → 翻转为 [4,3]。
- 第三组：[5] → 保持原样。
最终结果：[2,1,4,3,5]。

示例 2

输入：head = [1,2,3,4,5], k = 3 输出：[3,2,1,4,5]

分组：
- 第一组：[1,2,3] → 翻转为 [3,2,1]。
- 第二组：[4,5] → 保持原样。
最终结果：[3,2,1,4,5]。

示例 3

输入：head = [1], k = 1 输出：[1]

只有一个节点，不需要翻转。

时间和空间复杂度

时间复杂度

时间复杂度： $O(n)$，其中 $n$ 是链表的长度。每个节点最多访问两次：一次计数，一次翻转。

空间复杂度

空间复杂度： $O(1)$，仅使用了指针变量。

总结

优点： 使用迭代法实现了 $O(1)$ 的空间复杂度，并且通过哨兵节点简化了边界条件处理。
扩展： 如果需要递归实现，可以将每次翻转的逻辑递归调用，但递归深度可能导致空间复杂度为 $O(n/k)$。

138. 随机链表的复制

问题描述

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。深拷贝应该正好由 n 个全新节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

val：一个表示 Node.val 的整数。
random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

你的代码只接受原链表的头节点 head 作为传入参数。

示例 1：

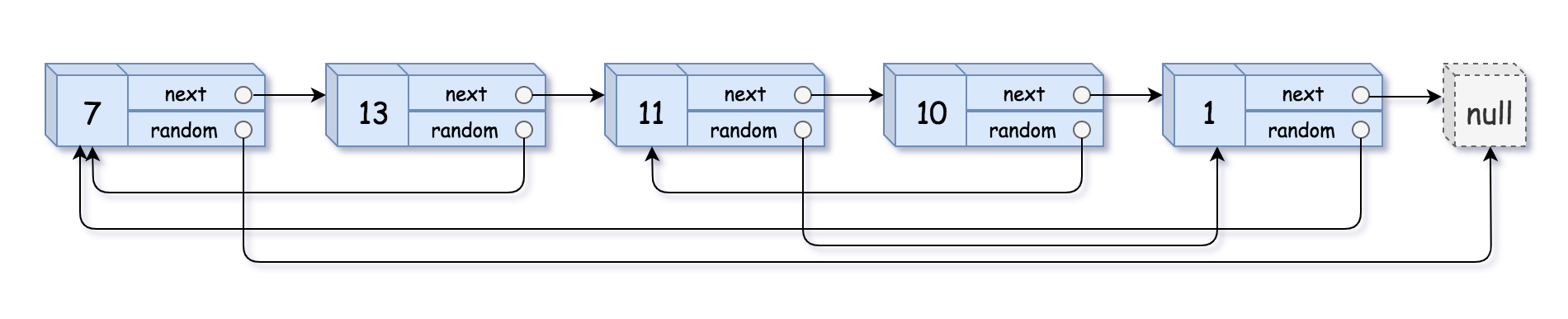
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例 2：

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

示例 3：

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

提示：

0 <= n <= 1000
$-10^4 <= Node.val <= 10^4$
Node.random 为 null 或指向链表中的节点。

题解

解题思路

为了复制一个带有随机指针的链表，需要实现一个 深拷贝，可以采用以下两种方法：

哈希表辅助法：
- 使用一个哈希表将原链表节点和新链表节点映射起来。
- 第一次遍历创建新节点并存储映射。
- 第二次遍历设置新链表节点的 next 和 random 指针。
原地拷贝法（优化空间复杂度）：
- 不使用额外空间，在原链表中插入新节点。
- 第一次遍历创建新节点并插入原链表。
- 第二次遍历设置 random 指针。
- 第三次遍历分离新链表和原链表。

下面详细介绍两种方法。

方法 1：哈希表辅助法

实现步骤

使用哈希表记录原节点和新节点的映射关系。
遍历链表创建新节点，并存入哈希表。
再次遍历链表，使用哈希表设置新节点的 next 和 random 指针。

C++ 实现

  
/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     Node* next;
 *     Node* random;
 *     Node(int _val) {
 *         val = _val;
 *         next = nullptr;
 *         random = nullptr;
 *     }
 * };
 */

class Solution {
public:
    Node* copyRandomList(Node* head) {
        if (!head) return nullptr;

        // 哈希表存储原节点到新节点的映射
        unordered_map<Node*, Node*> nodeMap;

        // 第一次遍历：创建新节点并存入哈希表
        Node* curr = head;
        while (curr) {
            nodeMap[curr] = new Node(curr->val);
            curr = curr->next;
        }

        // 第二次遍历：设置新节点的 next 和 random 指针
        curr = head;
        while (curr) {
            nodeMap[curr]->next = nodeMap[curr->next];
            nodeMap[curr]->random = nodeMap[curr->random];
            curr = curr->next;
        }

        return nodeMap[head];
    }
};

方法 2：原地拷贝法

实现步骤

在每个原节点后插入一个新节点，使链表变成交替排列。
遍历链表，设置新节点的 random 指针。
遍历链表，分离新链表和原链表。

C++ 实现

  
class Solution {
public:
    Node* copyRandomList(Node* head) {
        if (!head) return nullptr;

        // 第一步：在每个原节点后插入新节点
        Node* curr = head;
        while (curr) {
            Node* newNode = new Node(curr->val);
            newNode->next = curr->next;
            curr->next = newNode;
            curr = newNode->next;
        }

        // 第二步：设置新节点的 random 指针
        curr = head;
        while (curr) {
            if (curr->random) {
                curr->next->random = curr->random->next;
            }
            curr = curr->next->next;
        }

        // 第三步：分离新链表和原链表
        Node* newHead = head->next;
        curr = head;
        while (curr) {
            Node* newNode = curr->next;
            curr->next = newNode->next;
            if (newNode->next) {
                newNode->next = newNode->next->next;
            }
            curr = curr->next;
        }

        return newHead;
    }
};

示例讲解

示例 1

输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]] 输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

哈希表法：
- 第一次遍历：创建新节点并存储映射。
- 第二次遍历：利用映射设置 next 和 random。
原地拷贝法：
- 插入新节点：7 -> 7' -> 13 -> 13' -> ...
- 设置 random：新节点 random 指向对应复制的节点。
- 分离链表：分离新链表。

时间和空间复杂度

方法 1：哈希表辅助法

时间复杂度： $O(n)$，需要两次遍历链表。
空间复杂度： $O(n)$，哈希表存储节点映射。

方法 2：原地拷贝法

时间复杂度： $O(n)$，需要三次遍历链表。
空间复杂度： $O(1)$，只使用了常量空间。

总结

方法 1： 简单直观，但需要额外空间存储映射。
方法 2： 更高效，推荐在需要优化空间复杂度时使用。

148. 排序链表

问题描述

给你链表的头结点 head ，请将其按升序排列并返回 排序后的链表 。

示例 1：

输入：head = [4,2,1,3]
输出：[1,2,3,4]

示例 2：

输入：head = [-1,5,3,4,0]
输出：[-1,0,3,4,5]

示例 3：

输入：head = []
输出：[]

提示：

链表中节点的数目在范围 $[0, 5 * 10^4]$ 内
$-10^5 <= Node.val <= 10^5$

进阶：你可以在 O(n log n) 时间复杂度和常数级空间复杂度下，对链表进行排序吗？

题解

解题思路

要对链表进行排序，可以采用以下方法：

归并排序（推荐）：
- 归并排序的时间复杂度为 $O(n \log n)$，非常适合链表。
- 使用快慢指针将链表分成两半，然后递归地对两部分排序，最后合并两部分。
- 由于链表操作中插入和删除节点效率较高，归并排序是链表排序的理想选择。
快速排序：
- 快速排序不适合链表，因为链表无法直接访问中间节点，导致分区操作效率较低。

进阶要求： 使用 $O(1)$ 的额外空间进行排序，归并排序仍然可以满足这个条件。

归并排序的实现

实现步骤

分割链表：
- 使用快慢指针将链表分成两部分。
- 快指针每次走两步，慢指针每次走一步。
- 当快指针到达末尾时，慢指针正好在链表中间。
递归排序：
- 对两部分链表递归排序。
合并链表：
- 使用双指针将两个有序链表合并为一个新的有序链表。

C++ 代码实现

  
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */

class Solution {
public:
    ListNode* sortList(ListNode* head) {
        // 终止条件：链表为空或只有一个节点
        if (!head || !head->next) {
            return head;
        }

        // 1. 分割链表
        ListNode* mid = getMid(head);
        ListNode* left = head;
        ListNode* right = mid->next;
        mid->next = nullptr; // 分割链表

        // 2. 递归排序左右两部分
        left = sortList(left);
        right = sortList(right);

        // 3. 合并排序后的链表
        return merge(left, right);
    }

private:
    // 获取链表的中间节点
    ListNode* getMid(ListNode* head) {
        ListNode* slow = head;
        ListNode* fast = head->next;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
        }
        return slow;
    }

    // 合并两个有序链表
    ListNode* merge(ListNode* l1, ListNode* l2) {
        ListNode dummy; // 哨兵节点
        ListNode* curr = &dummy;

        while (l1 && l2) {
            if (l1->val <= l2->val) {
                curr->next = l1;
                l1 = l1->next;
            } else {
                curr->next = l2;
                l2 = l2->next;
            }
            curr = curr->next;
        }

        curr->next = l1 ? l1 : l2; // 连接剩余部分
        return dummy.next;
    }
};

示例讲解

示例 1

输入：head = [4,2,1,3] 输出：[1,2,3,4]

初始链表：4 -> 2 -> 1 -> 3
分割：[4,2] 和 [1,3]
递归排序：
- [4,2] → 分割为 [4] 和 [2] → 合并为 [2,4]
- [1,3] → 分割为 [1] 和 [3] → 合并为 [1,3]
合并：[2,4] 和 [1,3] → [1,2,3,4]

时间和空间复杂度

时间复杂度

时间复杂度： $O(n \log n)$，归并排序需要 $\log n$ 次分割，每次分割需要 $O(n)$ 的时间合并。

空间复杂度

空间复杂度： $O(1)$，使用了常量额外空间。
递归栈空间： $O(\log n)$，递归调用深度为 $\log n$。

总结

归并排序适合链表排序，因为其合并操作只需要指针操作。
在 $O(n \log n)$ 时间复杂度和 $O(1)$ 空间复杂度下，归并排序是最佳选择。

23. 合并K个升序链表

问题描述

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[] 

提示：

k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] 按升序排列
lists[i].length 的总和不超过 10^4

题解

解题思路

要将 $k$ 个升序链表合并为一个升序链表，可以采用以下几种方法：

逐一合并（顺序合并）：
- 两两合并链表，最后得到一个合并后的链表。
- 时间复杂度较高，不推荐。
分治法：
- 使用分治思想，每次将链表数组分成两部分，递归合并。
- 分治法可以显著降低时间复杂度，从 $O(k \times n)$ 降到 $O(n \log k)$。
最小堆（优先队列）：
- 使用最小堆（或优先队列）存储每个链表的当前头节点。
- 每次从堆中取最小值节点，并将其加入结果链表，同时将其后继节点加入堆。
- 时间复杂度为 O(nlog⁡k)O(n \log k)，适合处理大量链表。

方法 1：分治法

实现步骤

将链表数组分为两部分，递归合并每部分。
使用两个链表的合并函数（归并思想）合并分治后的结果。

C++ 实现

  
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */

class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        if (lists.empty()) return nullptr;
        return mergeKListsHelper(lists, 0, lists.size() - 1);
    }

private:
    // 分治合并链表
    ListNode* mergeKListsHelper(vector<ListNode*>& lists, int left, int right) {
        if (left == right) return lists[left]; // 只有一个链表，直接返回
        int mid = left + (right - left) / 2;
        ListNode* l1 = mergeKListsHelper(lists, left, mid);
        ListNode* l2 = mergeKListsHelper(lists, mid + 1, right);
        return mergeTwoLists(l1, l2);
    }

    // 合并两个链表
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        ListNode dummy; // 哨兵节点
        ListNode* current = &dummy;

        while (l1 && l2) {
            if (l1->val <= l2->val) {
                current->next = l1;
                l1 = l1->next;
            } else {
                current->next = l2;
                l2 = l2->next;
            }
            current = current->next;
        }

        current->next = l1 ? l1 : l2;
        return dummy.next;
    }
};

方法 2：最小堆（优先队列）

实现步骤

将所有链表的头节点加入最小堆（根据节点值排序）。
每次从堆中取出最小值节点，将其加入结果链表。
如果该节点有后继节点，将后继节点加入堆。
重复操作直到堆为空。

C++ 实现

  
#include <queue>
class Solution {
public:
    struct Compare {
        bool operator()(ListNode* a, ListNode* b) {
            return a->val > b->val;
        }
    };

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        priority_queue<ListNode*, vector<ListNode*>, Compare> pq;

        // 将所有链表的头节点加入堆
        for (auto node : lists) {
            if (node) pq.push(node);
        }

        ListNode dummy; // 哨兵节点
        ListNode* current = &dummy;

        while (!pq.empty()) {
            ListNode* smallest = pq.top();
            pq.pop();
            current->next = smallest;
            current = current->next;

            if (smallest->next) {
                pq.push(smallest->next);
            }
        }

        return dummy.next;
    }
};

示例讲解

示例 1

输入：lists = [[1,4,5],[1,3,4],[2,6]] 输出：[1,1,2,3,4,4,5,6]

使用分治法：
- 将 [[1,4,5],[1,3,4],[2,6]] 分成两部分。
- 合并 [1,4,5] 和 [1,3,4] → [1,1,3,4,4,5]。
- 合并 [1,1,3,4,4,5] 和 [2,6] → [1,1,2,3,4,4,5,6]。
使用最小堆：
- 初始堆：[1,1,2]。
- 每次取最小值并加入结果链表，同时将其后继节点加入堆。

时间和空间复杂度

方法 1：分治法

时间复杂度：
$O(n \log k)$，其中 $n$ 是链表总节点数，$k$ 是链表数量。
- 每次合并两个链表需要 $O(n/k)$，总共递归 $\log k$ 层。
空间复杂度： $O(\log k)$，递归调用栈的深度为 $\log k$。

方法 2：最小堆

时间复杂度： $O(n \log k)$，堆操作的时间复杂度为 $\log k$。
空间复杂度： $O(k)$，堆中最多存储 $k$ 个节点。

总结

分治法： 简洁清晰，适合一般场景。
最小堆： 对于 $k$ 很大时更高效，因为堆的操作规模与 $k$ 相关。

146. LRU缓存

问题描述

请你设计并实现一个满足 LRU (最近最少使用) 缓存约束的数据结构。

实现 LRUCache 类：

LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该逐出最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

提示：

1 <= capacity <= 3000
0 <= key <= 10000
$0 <= value <= 10^5$
最多调用 $2 * 10^5$ 次 get 和 put

题解

要实现 LRU 缓存，需要满足以下条件：

支持 $O(1)$ 的时间复杂度：
- get(key)：从缓存中获取值。
- put(key, value)：插入或更新值。
维护访问顺序： 按最近访问时间排序，淘汰最久未使用的元素。

解题思路

可以使用 哈希表 + 双向链表 实现：

哈希表： 用于存储键值对，支持快速查找。
双向链表：
维护缓存中元素的访问顺序：
- 最近访问的元素放在链表头部。
- 最久未使用的元素放在链表尾部。

操作实现

get(key)：
- 如果 key 存在于缓存：
  - 将对应的节点移到链表头部（表示最近使用）。
  - 返回节点的值。
- 如果 key 不存在，返回 -1。
put(key, value)：
- 如果 key 已存在：
  - 更新其值。
  - 将节点移到链表头部。
- 如果 key 不存在：
  - 如果缓存已满，移除链表尾部节点（最久未使用）。
  - 插入新节点到链表头部。

C++ 代码实现

  
#include <unordered_map>
using namespace std;

class LRUCache {
private:
    // 双向链表节点定义
    struct Node {
        int key, value;
        Node* prev;
        Node* next;
        Node(int k, int v) : key(k), value(v), prev(nullptr), next(nullptr) {}
    };

    unordered_map<int, Node*> cache; // 哈希表：key -> Node
    Node* head;                     // 虚拟头节点
    Node* tail;                     // 虚拟尾节点
    int capacity;                   // 缓存容量
    int size;                       // 当前缓存大小

    // 移动节点到链表头部
    void moveToHead(Node* node) {
        removeNode(node); // 先从链表中移除
        addToHead(node);  // 再添加到头部
    }

    // 添加节点到链表头部
    void addToHead(Node* node) {
        node->prev = head;
        node->next = head->next;
        head->next->prev = node;
        head->next = node;
    }

    // 删除链表中的节点
    void removeNode(Node* node) {
        node->prev->next = node->next;
        node->next->prev = node->prev;
    }

    // 移除链表尾部节点
    Node* removeTail() {
        Node* node = tail->prev;
        removeNode(node);
        return node;
    }

public:
    LRUCache(int capacity) : capacity(capacity), size(0) {
        head = new Node(0, 0); // 虚拟头节点
        tail = new Node(0, 0); // 虚拟尾节点
        head->next = tail;
        tail->prev = head;
    }

    ~LRUCache() {
        Node* curr = head;
        while (curr) {
            Node* temp = curr;
            curr = curr->next;
            delete temp;
        }
    }

    int get(int key) {
        if (cache.count(key)) {
            Node* node = cache[key];
            moveToHead(node); // 最近访问，移到链表头部
            return node->value;
        }
        return -1; // 不存在
    }

    void put(int key, int value) {
        if (cache.count(key)) {
            Node* node = cache[key];
            node->value = value; // 更新值
            moveToHead(node);    // 移到链表头部
        } else {
            Node* newNode = new Node(key, value);
            cache[key] = newNode;
            addToHead(newNode); // 插入到链表头部
            size++;
            if (size > capacity) { // 缓存已满
                Node* tailNode = removeTail(); // 移除尾部节点
                cache.erase(tailNode->key);   // 从哈希表中删除
                delete tailNode;
                size--;
            }
        }
    }
};

示例讲解

示例 1

输入：

["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]

输出：

[null, null, null, 1, null, -1, null, -1, 3, 4]

操作解析：

put(1, 1)：缓存为 {1=1}。
put(2, 2)：缓存为 {1=1, 2=2}。
get(1)：返回 1，缓存变为 {2=2, 1=1}。
put(3, 3)：缓存满了，移除最久未使用的键 2，缓存为 {1=1, 3=3}。
get(2)：返回 -1。
put(4, 4)：缓存满了，移除最久未使用的键 1，缓存为 {3=3, 4=4}。
get(1)：返回 -1。
get(3)：返回 3。
get(4)：返回 4。

时间和空间复杂度

时间复杂度

get 和 put： $O(1)$，哈希表和双向链表的操作均为常数时间。

空间复杂度

空间复杂度： $O(capacity)$，存储至多 $capacity$ 个缓存元素。

总结

哈希表 + 双向链表 是实现 LRU 缓存的最佳组合，既满足 $O(1)$ 的时间复杂度，又能够维护最近使用顺序。
对于大规模缓存，推荐使用类似的实现方式，具有高效性和可扩展性。

leetcode, hot100

本文由作者按照 CC BY 4.0 进行授权