hot100二叉树2题解

发表于 2025/01/17 更新于 2025/01/17

作者 匆匆那年 36 分钟阅读

230. 二叉搜索树中第K小的元素

问题描述

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

示例 1：

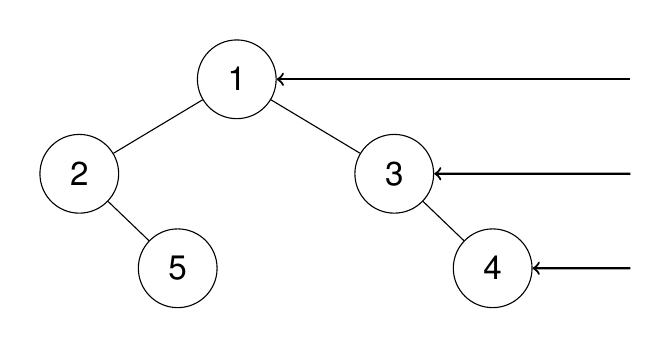
输入：root = [3,1,4,null,2], k = 1
输出：1

示例 2：

输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：3

提示：

树中的节点数为 n 。
$1 <= k <= n <= 10^4$
$0 <= Node.val <= 10^4$

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

题解

以下是 LeetCode 230. 二叉搜索树中第 K 小的元素 的 C++ 解法，包括两种实现方式：直接中序遍历和维护节点计数的优化方案。

方法 1：中序遍历（适用于静态树）

核心思路：

二叉搜索树的中序遍历会生成一个有序的节点序列。
遍历过程中，计数到第 $k$ 个节点时，直接返回该节点值。

代码实现：

  
class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        stack<TreeNode*> s;
        while (!s.empty() || root) {
            // 左子树全部入栈
            while (root) {
                s.push(root);
                root = root->left;
            }

            // 访问栈顶节点
            root = s.top();
            s.pop();

            // 递减 k，检查是否为第 k 个节点
            if (--k == 0) {
                return root->val;
            }

            // 转向右子树
            root = root->right;
        }
        return -1; // 不会到达此处，因为题目保证 k 有效
    }
};

方法 2：维护节点计数的优化（适用于动态树）

核心思路：

在每个节点上存储其左子树的节点数 leftCount。
使用 leftCount 判断目标节点是否在左子树、当前节点或右子树中：
1. 如果 $k \leq \text{leftCount}$，目标在左子树。
2. 如果 $k = \text{leftCount} + 1$，当前节点是目标。
3. 如果 $k > \text{leftCount} + 1$，目标在右子树，调整 $k = k - \text{leftCount} - 1$。

代码实现：

  
class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    int leftCount; // 左子树节点数

    TreeNode(int x) : val(x), left(nullptr), right(nullptr), leftCount(0) {}
};

class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        while (root) {
            if (root->leftCount + 1 == k) {
                return root->val; // 当前节点是第 k 小元素
            } else if (k <= root->leftCount) {
                root = root->left; // 目标在左子树
            } else {
                k -= root->leftCount + 1; // 调整 k 并搜索右子树
                root = root->right;
            }
        }
        return -1; // 不会到达此处，因为题目保证 k 有效
    }
};

节点计数更新：

在树插入或删除时，动态维护每个节点的 leftCount 值。

代码分析

方法 1：中序遍历

时间复杂度: $O(k)$，中序遍历过程中最多访问 $k$ 个节点。
空间复杂度: $O(h)$，栈的最大深度为树的高度 $h$。

方法 2：节点计数优化

时间复杂度: $O(h)$，每次查询的复杂度与树的高度 $h$ 成正比。
空间复杂度: $O(1)$，无需额外的栈空间。
适用场景: 动态修改频繁的场景。

示例运行

示例 1

输入：

root = [3,1,4,null,2], k = 1

输出：

1

示例 2

输入：

root = [5,3,6,2,4,null,null,1], k = 3

输出：

3

进阶思考

在需要频繁查找第 $k$ 小值的动态树中，维护节点计数可以显著提高效率。
如果修改操作较少且查找较频繁，方法 1（中序遍历）依然是简单且高效的选择。

199. 二叉树的右视图

问题描述

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1：

输入：root = [1,2,3,null,5,null,4]

输出：[1,3,4]

解释：

示例 2：

输入：root = [1,2,3,4,null,null,null,5]

输出：[1,3,4,5]

解释：

示例 3：

输入：root = [1,null,3]

输出：[1,3]

示例 4：

输入：root = []

输出：[]

提示:

二叉树的节点个数的范围是 [0,100]
-100 <= Node.val <= 100

题解

以下是 LeetCode 199. 二叉树的右视图 的 C++ 解法，分别通过广度优先搜索（BFS）和深度优先搜索（DFS）实现。

方法 1：广度优先搜索（BFS）

利用层序遍历，每层从左到右遍历节点，将每层的最后一个节点值加入结果。

核心逻辑：

使用队列进行层序遍历。
每层从左到右依次访问节点，将每层的最后一个节点的值加入结果。

代码实现：

  
#include <queue>
#include <vector>
using namespace std;

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> result;
        if (root == nullptr) return result;

        queue<TreeNode*> q;
        q.push(root);

        while (!q.empty()) {
            int levelSize = q.size(); // 当前层的节点数量
            for (int i = 0; i < levelSize; ++i) {
                TreeNode* node = q.front();
                q.pop();

                // 如果是当前层的最后一个节点，加入结果
                if (i == levelSize - 1) {
                    result.push_back(node->val);
                }

                // 将左右子节点加入队列
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
        }

        return result;
    }
};

方法 2：深度优先搜索（DFS）

通过先访问右子树的递归遍历，保证优先处理右边的节点，每层只保留第一个被访问的节点。

核心逻辑：

使用一个深度变量 level 跟踪当前层数。
如果当前层的结果还未存储，将当前节点值加入结果。
递归优先访问右子树，再访问左子树。

代码实现：

  
#include <vector>
using namespace std;

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        vector<int> result;
        dfs(root, 0, result);
        return result;
    }

private:
    void dfs(TreeNode* node, int level, vector<int>& result) {
        if (node == nullptr) return;

        // 如果当前层还没有记录值，添加节点值
        if (level == result.size()) {
            result.push_back(node->val);
        }

        // 优先访问右子树
        dfs(node->right, level + 1, result);
        // 再访问左子树
        dfs(node->left, level + 1, result);
    }
};

代码分析

方法 1：BFS

时间复杂度: $O(n)$，每个节点访问一次。
空间复杂度: $O(w)$，其中 $w$ 是树的最大宽度，队列的最大元素数。

方法 2：DFS

时间复杂度: $O(n)$，每个节点访问一次。
空间复杂度: $O(h)$，其中 $h$ 是树的高度，递归调用栈的深度。

示例运行

示例 1

输入：

root = [1,2,3,null,5,null,4]

输出：

[1,3,4]

示例 2

输入：

root = [1,2,3,4,null,null,null,5]

输出：

[1,3,4,5]

示例 3

输入：

root = [1,null,3]

输出：

[1,3]

方法选择

BFS 更适合于层序处理任务，逻辑直观。
DFS 在需要递归控制的场景下更简洁，适合需要优先处理某些子树的场景。

114. 二叉树展开为链表

问题描述

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。

示例 1：

输入：root = [1,2,5,3,4,null,6]
输出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [0]
输出：[0]

提示：

树中结点数在范围 [0, 2000] 内
-100 <= Node.val <= 100

进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

题解

题解：二叉树展开为链表 (C++)

方法一：递归 + 原地修改

利用递归的方式，我们可以按照先序遍历的顺序展开二叉树。在递归过程中，逐步将左子树展开为链表，并将其拼接到右子树之前。

C++ 实现

  
#include <iostream>
using namespace std;

// 定义二叉树节点
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    void flatten(TreeNode* root) {
        if (!root) return;

        // 递归展开左子树和右子树
        flatten(root->left);
        flatten(root->right);

        // 保存右子树
        TreeNode* rightSubtree = root->right;

        // 将左子树移到右子树的位置
        root->right = root->left;
        root->left = nullptr;

        // 找到当前右子树的末尾
        TreeNode* current = root;
        while (current->right) {
            current = current->right;
        }

        // 将保存的右子树连接到末尾
        current->right = rightSubtree;
    }
};

方法二：迭代 + 原地修改

通过迭代的方法，我们可以使用 while 循环以原地方式展开二叉树，而无需递归。

C++ 实现

  
class Solution {
public:
    void flatten(TreeNode* root) {
        TreeNode* current = root;

        while (current) {
            if (current->left) {
                // 找到左子树的最右节点
                TreeNode* pre = current->left;
                while (pre->right) {
                    pre = pre->right;
                }

                // 将右子树连接到左子树的最右节点
                pre->right = current->right;

                // 将左子树移到右边
                current->right = current->left;
                current->left = nullptr;
            }

            // 移动到下一个节点
            current = current->right;
        }
    }
};

方法三：逆向后序遍历

从右子树和左子树逆序进行处理，可以保证每次访问到的节点已经是链表的一部分。

C++ 实现

  
class Solution {
public:
    void flatten(TreeNode* root) {
        TreeNode* prev = nullptr;

        // 逆后序遍历
        function<void(TreeNode*)> postOrder = [&](TreeNode* node) {
            if (!node) return;

            postOrder(node->right);
            postOrder(node->left);

            // 修改指针
            node->right = prev;
            node->left = nullptr;
            prev = node;
        };

        postOrder(root);
    }
};

解题思路总结

递归方法：自顶向下，递归处理左右子树，将左子树拼接到右子树上。
迭代方法：使用 while 循环，找到左子树最右节点，并调整指针。
逆向后序遍历：从右子树开始逆序调整指针，确保每次的右指针指向链表的下一个节点。

选择不同方法取决于习惯和性能需求。这三种方法都能实现 O(1) 额外空间展开，并保持先序遍历顺序。

105. 从前序与中序遍历序列构造二叉树

问题描述

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

题解

解题思路

构造二叉树的核心思路是利用以下性质：

前序遍历的第一个元素是当前树的根节点。
中序遍历中，根节点将序列分为左子树和右子树。
- 根节点左侧的元素为左子树的节点。
- 根节点右侧的元素为右子树的节点。

通过递归，我们可以根据上述特性逐步构造整棵树。

C++ 实现

  
#include <iostream>
#include <unordered_map>
#include <vector>
using namespace std;

// 定义二叉树节点
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        // 哈希表存储中序遍历每个值对应的索引位置
        unordered_map<int, int> inorderIndex;
        for (int i = 0; i < inorder.size(); ++i) {
            inorderIndex[inorder[i]] = i;
        }

        // 递归构建二叉树
        return buildSubTree(preorder, 0, preorder.size() - 1, inorder, 0, inorder.size() - 1, inorderIndex);
    }

private:
    TreeNode* buildSubTree(
        vector<int>& preorder, int preStart, int preEnd,
        vector<int>& inorder, int inStart, int inEnd,
        unordered_map<int, int>& inorderIndex) {

        // 递归终止条件：如果索引越界，返回空节点
        if (preStart > preEnd || inStart > inEnd) {
            return nullptr;
        }

        // 从前序遍历找到根节点
        int rootVal = preorder[preStart];
        TreeNode* root = new TreeNode(rootVal);

        // 从中序遍历中找到根节点的位置
        int rootIndex = inorderIndex[rootVal];
        int leftTreeSize = rootIndex - inStart;

        // 递归构建左子树和右子树
        root->left = buildSubTree(preorder, preStart + 1, preStart + leftTreeSize,
                                  inorder, inStart, rootIndex - 1, inorderIndex);
        root->right = buildSubTree(preorder, preStart + leftTreeSize + 1, preEnd,
                                   inorder, rootIndex + 1, inEnd, inorderIndex);

        return root;
    }
};

示例运行

  
int main() {
    Solution solution;
    vector<int> preorder = {3, 9, 20, 15, 7};
    vector<int> inorder = {9, 3, 15, 20, 7};

    TreeNode* root = solution.buildTree(preorder, inorder);

    // 简单测试输出树的结构
    // 使用简单的 BFS 或其他方法打印验证树结构
    return 0;
}

解题思路总结

使用递归：
- 前序遍历确定根节点。
- 中序遍历分割左右子树。
- 递归构建左右子树。
优化：
- 使用哈希表快速定位中序遍历的索引，减少查找时间复杂度。
时间复杂度：
- 构建哈希表：$O(n)$
- 构造二叉树：$O(n)$
- 总复杂度：$O(n)$
空间复杂度：
- 哈希表：$O(n)$
- 递归调用栈：最差 $O(n)$（树退化为链表）。
- 总空间复杂度：$O(n)$。

437. 路径总和 III

问题描述

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的路径的数目。

路径不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：

输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2：

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

提示:

二叉树的节点个数的范围是 [0,1000]
$-10^9 <= Node.val <= 10^9$
-1000 <= targetSum <= 1000

题解

本题的目标是找到所有路径和等于 targetSum 的路径数量。路径可以从树的任何节点开始，但必须向下延伸。

解题思路

我们可以通过以下方法解决该问题：

方法一：暴力递归

对于每个节点，计算以该节点为起点的所有路径和，递归地对左右子树进行相同操作。每个节点都作为路径起点进行一次计算。

使用一个辅助函数计算以当前节点为起点的路径数量。
对每个节点重复上述操作，求路径总数。

时间复杂度：

对每个节点调用辅助函数，计算路径和。
时间复杂度约为 $O(n^2)$（最差情况下，完全二叉树）。

方法二：前缀和 + 哈希表

使用前缀和的思想记录路径和，可以有效减少时间复杂度。

使用一个哈希表记录从根节点到当前节点路径和的出现次数。
对于每个节点，计算从任意祖先节点到当前节点的路径和是否等于 targetSum。
- 当前路径和为 currSum，则需要查找 currSum - targetSum 是否在哈希表中。
在递归过程中维护哈希表，回溯时及时更新。

时间复杂度：

每个节点仅访问一次，时间复杂度为 $O(n)$。

C++ 实现

方法一：暴力递归

  
#include <iostream>
#include <vector>
using namespace std;

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    long long pathSum(TreeNode* root, int targetSum) {
        if (!root) return 0;
        // 以当前节点为起点的路径数 + 左子树的路径数 + 右子树的路径数
        return pathSumFromNode(root, targetSum) + 
               pathSum(root->left, targetSum) + 
               pathSum(root->right, targetSum);
    }

private:
    long long pathSumFromNode(TreeNode* node, long long targetSum) {
        if (!node) return 0;

        // 当前节点能构成的路径数
        long long count = (node->val == targetSum) ? 1 : 0;

        // 继续向下查找路径
        count += pathSumFromNode(node->left, targetSum - node->val);
        count += pathSumFromNode(node->right, targetSum - node->val);

        return count;
    }
};

方法二：前缀和 + 哈希表

  
#include <unordered_map>
class Solution {
public:
    int pathSum(TreeNode* root, int targetSum) {
        unordered_map<long long, int> prefixSumCount;
        // 初始化前缀和为 0 的路径数量为 1
        prefixSumCount[0] = 1;
        return dfs(root, 0, targetSum, prefixSumCount);
    }

private:
    int dfs(TreeNode* node, long long currSum, int targetSum, unordered_map<long long, int>& prefixSumCount) {
        if (!node) return 0;

        // 当前路径和
        currSum += node->val;

        // 查找满足条件的路径数
        int count = prefixSumCount[currSum - targetSum];

        // 更新前缀和计数
        prefixSumCount[currSum]++;

        // 递归处理左右子树
        count += dfs(node->left, currSum, targetSum, prefixSumCount);
        count += dfs(node->right, currSum, targetSum, prefixSumCount);

        // 回溯，撤销当前节点对前缀和的影响
        prefixSumCount[currSum]--;

        return count;
    }
};

示例运行

  
int main() {
    Solution solution;

    // 构造测试二叉树
    TreeNode* root = new TreeNode(10);
    root->left = new TreeNode(5);
    root->right = new TreeNode(-3);
    root->left->left = new TreeNode(3);
    root->left->right = new TreeNode(2);
    root->right->right = new TreeNode(11);
    root->left->left->left = new TreeNode(3);
    root->left->left->right = new TreeNode(-2);
    root->left->right->right = new TreeNode(1);

    int targetSum = 8;

    cout << "Number of paths: " << solution.pathSum(root, targetSum) << endl;

    return 0;
}

解题思路总结

暴力递归适合简单情况，但在节点较多时效率低。
前缀和 + 哈希表大幅优化时间复杂度，推荐使用。
回溯技巧在前缀和方法中用于撤销递归的影响，避免多余计算。

时间复杂度对比：

暴力递归：最差 $O(n^2)$
前缀和：$O(n)$

236. 二叉树的最近公共祖先

问题描述

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

示例 2：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

提示：

树中节点数目在范围 $[2, 10^5]$ 内。
$-10^9 <= Node.val <= 10^9$
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。

题解

解题思路

利用二叉树的递归特性，从根节点开始查找 p 和 q 的最近公共祖先。分以下几种情况：

如果当前节点为 nullptr，返回 nullptr。
如果当前节点是 p 或 q，直接返回当前节点。
对左右子树递归查找：
- 如果左右子树分别返回非空值，说明当前节点是最近公共祖先。
- 如果只有一边返回非空值，则最近公共祖先在返回的这一侧。

C++ 实现

递归方法

  
#include <iostream>
using namespace std;

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        // 如果当前节点为 nullptr 或为 p 或 q，则直接返回
        if (!root || root == p || root == q) {
            return root;
        }

        // 递归查找左子树和右子树
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);

        // 如果左右子树都找到节点，说明当前节点是最近公共祖先
        if (left && right) {
            return root;
        }

        // 否则返回非空的那一侧
        return left ? left : right;
    }
};

示例运行

  
int main() {
    // 构造示例树
    TreeNode* root = new TreeNode(3);
    root->left = new TreeNode(5);
    root->right = new TreeNode(1);
    root->left->left = new TreeNode(6);
    root->left->right = new TreeNode(2);
    root->right->left = new TreeNode(0);
    root->right->right = new TreeNode(8);
    root->left->right->left = new TreeNode(7);
    root->left->right->right = new TreeNode(4);

    Solution solution;
    TreeNode* p = root->left;         // 节点 5
    TreeNode* q = root->right;        // 节点 1

    TreeNode* lca = solution.lowestCommonAncestor(root, p, q);
    cout << "最近公共祖先节点值: " << lca->val << endl;

    return 0;
}

时间复杂度和空间复杂度

时间复杂度：
- 每个节点仅访问一次，时间复杂度为 $O(n)$，其中 $n$ 是节点数量。
空间复杂度：
- 递归调用栈的空间复杂度取决于树的高度，最差情况 $O(n)$（链表型树），最好情况 $O(\log n)$（平衡二叉树）。

关键点解析

递归终止条件：
- 当找到 nullptr 或目标节点 p 或 q 时，返回当前节点。
左右子树的结果处理：
- 如果左右子树都不为空，说明 p 和 q 分布在当前节点的两侧，此时当前节点为最近公共祖先。
- 如果一侧为空，说明 p 和 q 均在另一侧。
性能优化：
- 该方法保证每个节点只访问一次，适合较大的树。

总结

此递归方法逻辑清晰，性能高效，是解决二叉树最近公共祖先问题的经典方案。

124. 二叉树中的最大路径和

问题描述

二叉树中的路径被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 $[1, 3 * 10^4]$
-1000 <= Node.val <= 1000

题解

本题要求找到二叉树中任意路径的最大路径和。路径可以从任意节点开始并到任意节点结束。

解题思路

我们可以使用 后序遍历 + 动态规划 的方式解决问题。对每个节点，计算通过该节点的最大路径和，并更新全局最大值。

定义与递归

定义单边路径和：
- 单边路径和是从当前节点延伸至左子树或右子树的路径和。
- 递归函数返回单边路径和（即某节点为起点的最大贡献值）。
通过当前节点的路径和：
- 当前节点的路径和是节点值加上左子树单边路径和和右子树单边路径和。
- 使用该值更新全局最大路径和。
递归公式：
- 对于节点 root：
  - 左子树的最大单边路径和：left = max(0, dfs(root->left))
  - 右子树的最大单边路径和：right = max(0, dfs(root->right))
  - 当前路径和：currentPathSum = root->val + left + right
  - 更新全局最大路径和。
  - 返回单边路径和：root->val + max(left, right)。

C++ 实现

  
#include <iostream>
#include <algorithm>
#include <limits.h>
using namespace std;

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

class Solution {
public:
    int maxPathSum(TreeNode* root) {
        int maxSum = INT_MIN; // 全局最大路径和
        dfs(root, maxSum);
        return maxSum;
    }

private:
    int dfs(TreeNode* node, int& maxSum) {
        if (!node) return 0;

        // 计算左右子树的单边最大路径和（不选择负数路径）
        int left = max(0, dfs(node->left, maxSum));
        int right = max(0, dfs(node->right, maxSum));

        // 通过当前节点的路径和
        int currentPathSum = node->val + left + right;

        // 更新全局最大路径和
        maxSum = max(maxSum, currentPathSum);

        // 返回当前节点的单边最大路径和
        return node->val + max(left, right);
    }
};

示例运行

  
int main() {
    Solution solution;

    // 示例 1
    TreeNode* root1 = new TreeNode(1);
    root1->left = new TreeNode(2);
    root1->right = new TreeNode(3);
    cout << "最大路径和 (示例 1): " << solution.maxPathSum(root1) << endl;

    // 示例 2
    TreeNode* root2 = new TreeNode(-10);
    root2->left = new TreeNode(9);
    root2->right = new TreeNode(20);
    root2->right->left = new TreeNode(15);
    root2->right->right = new TreeNode(7);
    cout << "最大路径和 (示例 2): " << solution.maxPathSum(root2) << endl;

    return 0;
}

时间复杂度和空间复杂度

时间复杂度：
- 每个节点仅访问一次，时间复杂度为 $O(n)$，其中 $n$ 是节点数。
空间复杂度：
- 递归调用栈的深度为树的高度，最差 $O(n)$（链表型树），平均 $O(\log n)$（平衡二叉树）。

示例结果

示例 1： 输入树为 [1, 2, 3]，最优路径为 2 -> 1 -> 3，路径和为 6。

示例 2： 输入树为 [-10, 9, 20, null, null, 15, 7]，最优路径为 15 -> 20 -> 7，路径和为 42。

总结

递归函数计算的是单边最大路径和。
全局最大值记录的是当前遍历节点的最大路径和。
通过分治和动态规划的思想，本题可在 $O(n)$ 时间内高效解决。

leetcode, hot100

本文由作者按照 CC BY 4.0 进行授权