hot100二叉树1题解

94. 二叉树的中序遍历

问题描述

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例 1：

输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

题解

以下是 LeetCode 94. 二叉树的中序遍历 的 C++ 解法，包括递归和迭代两种方法：

---

方法 1：递归实现

递归方式是中序遍历的经典实现，按照 “左-根-右” 的顺序依次访问节点。

class Solution {
public:
    void inorderTraversalHelper(TreeNode* root, vector<int>& result) {
        if (root == nullptr) return;
        inorderTraversalHelper(root->left, result); // 访问左子树
        result.push_back(root->val);               // 访问根节点
        inorderTraversalHelper(root->right, result); // 访问右子树
    }

    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        inorderTraversalHelper(root, result);
        return result;
    }
};

---

方法 2：迭代实现

迭代方式使用栈模拟递归，按照 “左-根-右” 的顺序访问节点。

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> s;
        TreeNode* curr = root;

        while (curr != nullptr || !s.empty()) {
            // 将当前节点的所有左子树入栈
            while (curr != nullptr) {
                s.push(curr);
                curr = curr->left;
            }
            // 弹出栈顶节点
            curr = s.top();
            s.pop();
            result.push_back(curr->val); // 访问节点

            // 转向右子树
            curr = curr->right;
        }

        return result;
    }
};

---

代码分析

递归方法

1. 时间复杂度: $O(n)$，每个节点访问一次。
2. 空间复杂度: $O(h)$，$h$ 是树的高度，递归栈的深度。

迭代方法

1. 时间复杂度: $O(n)$，每个节点访问一次。
2. 空间复杂度: $O(h)$，$h$ 是树的高度，栈的最大深度。

---

示例运行

输入：

root = [1, null, 2, 3]

输出：

[1, 3, 2]

无论是递归还是迭代方法，输出结果相同。

104. 二叉树的最大深度

问题描述

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

• 树中节点的数量在 $[0, 10^4]$ 区间内。
• -100 <= Node.val <= 100

题解

以下是 LeetCode 104. 二叉树的最大深度 的 C++ 解法，包括递归和迭代两种方法：

---

方法 1：递归实现

递归是解决树相关问题的自然选择。通过分别求出左右子树的最大深度，然后取其较大值加 1。

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) {
            return 0; // 空树深度为 0
        }
        // 左子树和右子树深度的最大值加 1
        return 1 + max(maxDepth(root->left), maxDepth(root->right));
    }
};

---

方法 2：迭代实现（使用队列）

可以通过层序遍历（BFS）来计算树的深度，每遍历一层就增加深度计数。

#include <queue>

class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root == nullptr) {
            return 0; // 空树深度为 0
        }

        queue<TreeNode*> q;
        q.push(root);
        int depth = 0;

        while (!q.empty()) {
            int size = q.size(); // 当前层的节点数
            for (int i = 0; i < size; ++i) {
                TreeNode* node = q.front();
                q.pop();
                // 将下一层的节点加入队列
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
            ++depth; // 每遍历一层，深度加 1
        }

        return depth;
    }
};

---

代码分析

递归方法

1. 时间复杂度: $O(n)$，每个节点访问一次。
2. 空间复杂度: $O(h)$，$h$ 是树的高度，递归栈的深度。

迭代方法

1. 时间复杂度: $O(n)$，每个节点访问一次。
2. 空间复杂度: $O(w)$，$w$ 是树的最大宽度，队列中存储的最大节点数。

---

示例运行

输入：

root = [3,9,20,null,null,15,7]

递归输出：

3

迭代输出：

3

两种方法的输出结果相同。

226. 翻转二叉树

问题描述

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目范围在 [0, 100] 内
• -100 <= Node.val <= 100

题解

以下是 LeetCode 226. 翻转二叉树 的 C++ 解法，包括递归和迭代两种方法：

---

方法 1：递归实现

通过递归实现翻转二叉树，对每个节点的左右子树进行交换，然后递归处理其子节点。

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) {
            return nullptr; // 空树直接返回
        }
        // 交换左右子树
        TreeNode* temp = root->left;
        root->left = root->right;
        root->right = temp;

        // 递归处理左右子树
        invertTree(root->left);
        invertTree(root->right);

        return root;
    }
};

---

方法 2：迭代实现（使用队列）

可以使用广度优先搜索（BFS），利用队列实现翻转。每次访问一个节点时，交换其左右子树，并将子节点加入队列。

#include <queue>

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) {
            return nullptr; // 空树直接返回
        }

        queue<TreeNode*> q;
        q.push(root);

        while (!q.empty()) {
            TreeNode* node = q.front();
            q.pop();

            // 交换左右子树
            TreeNode* temp = node->left;
            node->left = node->right;
            node->right = temp;

            // 将左右子节点加入队列
            if (node->left) q.push(node->left);
            if (node->right) q.push(node->right);
        }

        return root;
    }
};

---

方法 3：迭代实现（使用栈）

通过深度优先搜索（DFS）使用栈实现翻转。每次访问一个节点时，交换其左右子树，并将子节点加入栈中。

#include <stack>

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) {
            return nullptr; // 空树直接返回
        }

        stack<TreeNode*> s;
        s.push(root);

        while (!s.empty()) {
            TreeNode* node = s.top();
            s.pop();

            // 交换左右子树
            TreeNode* temp = node->left;
            node->left = node->right;
            node->right = temp;

            // 将左右子节点加入栈
            if (node->left) s.push(node->left);
            if (node->right) s.push(node->right);
        }

        return root;
    }
};

---

代码分析

递归方法

1. 时间复杂度: $O(n)$，每个节点访问一次。
2. 空间复杂度: $O(h)$，$h$ 是树的高度，递归栈的深度。

迭代方法（队列和栈）

1. 时间复杂度: $O(n)$，每个节点访问一次。
2. 空间复杂度: $O(w)$，$w$ 是树的最大宽度（队列或栈的最大元素数）。

---

示例运行

输入：

root = [4,2,7,1,3,6,9]

递归输出：

[4,7,2,9,6,3,1]

迭代（队列）输出：

[4,7,2,9,6,3,1]

迭代（栈）输出：

[4,7,2,9,6,3,1]

所有方法的输出结果相同，具体可根据需求选择递归或迭代方案。

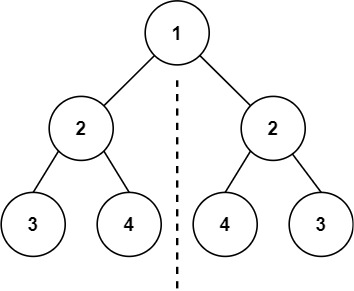
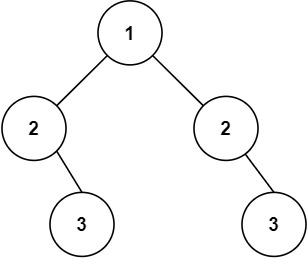
101. 对称二叉树

问题描述

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

题解

以下是 LeetCode 101. 对称二叉树 的 C++ 解法，包括递归和迭代两种方法：

---

方法 1：递归实现

通过递归比较左右子树，判断它们是否互为镜像。

核心逻辑：

1. 左子树的左子树和右子树的右子树相等。
2. 左子树的右子树和右子树的左子树相等。

class Solution {
public:
    bool isMirror(TreeNode* t1, TreeNode* t2) {
        if (t1 == nullptr && t2 == nullptr) return true; // 两个都是空，说明对称
        if (t1 == nullptr || t2 == nullptr) return false; // 一个空一个不空，不对称
        return (t1->val == t2->val)                      // 根节点值相等
            && isMirror(t1->left, t2->right)             // 左对右
            && isMirror(t1->right, t2->left);            // 右对左
    }

    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) return true;
        return isMirror(root->left, root->right);
    }
};

---

方法 2：迭代实现

使用队列进行层序遍历，同时将成对的节点加入队列，判断它们是否对称。

核心逻辑：

1. 初始将根的左右子树加入队列。
2. 每次从队列中取出两个节点，比较它们的值。
3. 如果相等，将它们的子节点成对加入队列（左-右、右-左）。
4. 如果不相等，返回 false。

#include <queue>

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) return true;

        queue<TreeNode*> q;
        q.push(root->left);
        q.push(root->right);

        while (!q.empty()) {
            TreeNode* t1 = q.front(); q.pop();
            TreeNode* t2 = q.front(); q.pop();

            if (t1 == nullptr && t2 == nullptr) continue; // 都是空，继续
            if (t1 == nullptr || t2 == nullptr) return false; // 一个空一个非空
            if (t1->val != t2->val) return false; // 值不相等，不对称

            // 按对称顺序加入队列
            q.push(t1->left);
            q.push(t2->right);
            q.push(t1->right);
            q.push(t2->left);
        }

        return true;
    }
};

---

代码分析

递归方法

1. 时间复杂度: $O(n)$，每个节点访问一次。
2. 空间复杂度: $O(h)$，$h$ 是树的高度，递归栈的深度。

迭代方法

1. 时间复杂度: $O(n)$，每个节点访问一次。
2. 空间复杂度: $O(w)$，$w$ 是树的最大宽度，队列中存储的最大节点数。

---

示例运行

输入：

root = [1,2,2,3,4,4,3]

递归输出：

true

迭代输出：

true

输入：

root = [1,2,2,null,3,null,3]

递归输出：

false

迭代输出：

false

两种方法均可以正确判断是否为对称二叉树，选择递归或迭代方案视个人需求而定。

543. 二叉树的直径

问题描述

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

提示：

• 树中节点数目在范围 $[1, 10^4]$ 内
• -100 <= Node.val <= 100

题解

以下是 LeetCode 543. 二叉树的直径 的 C++ 解法，通过递归计算二叉树的直径。

---

方法：递归实现

通过递归计算每个节点的左右子树的深度，直径是左右子树深度之和的最大值。

核心逻辑

1. 对于任意节点，左右子树的深度之和是经过该节点的路径长度。
2. 递归计算每个节点的左右子树深度，同时更新最大直径。
3. 返回节点的深度（1 + max(左子树深度, 右子树深度)）。

代码实现

class Solution {
public:
    int maxDiameter = 0; // 用于存储全局的最大直径

    int depth(TreeNode* root) {
        if (root == nullptr) return 0; // 空节点深度为 0

        // 递归计算左右子树深度
        int leftDepth = depth(root->left);
        int rightDepth = depth(root->right);

        // 更新最大直径
        maxDiameter = max(maxDiameter, leftDepth + rightDepth);

        // 返回当前节点的深度
        return 1 + max(leftDepth, rightDepth);
    }

    int diameterOfBinaryTree(TreeNode* root) {
        depth(root); // 计算深度的同时更新直径
        return maxDiameter;
    }
};

---

代码分析

1. 时间复杂度: $O(n)$，其中 $n$ 是节点数目，每个节点访问一次。
2. 空间复杂度: $O(h)$，其中 $h$ 是树的高度，递归调用栈的深度。

---

示例运行

示例 1

输入：

root = [1,2,3,4,5]

输出：

3

解释： 最长路径是 [4, 2, 1, 3] 或 [5, 2, 1, 3]，长度为 3。

---

示例 2

输入：

root = [1,2]

输出：

1

解释： 最长路径是 [2, 1]，长度为 1。

---

提示

• 边 的数量是节点数量减 1，所以直径等于最长路径的边数。
• 此方法一次递归即可完成计算，无需额外的遍历，是最优解法。

102. 二叉树的层序遍历

问题描述

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 [0, 2000] 内
• -1000 <= Node.val <= 1000

题解

以下是 LeetCode 102. 二叉树的层序遍历 的 C++ 解法，使用迭代（BFS）和递归两种方法实现。

---

方法 1：迭代实现（使用队列）

利用队列进行广度优先搜索（BFS），逐层遍历二叉树。

核心逻辑：

1. 初始化一个队列，将根节点加入队列。
2. 每次处理队列中的所有节点（即当前层的所有节点），将它们的值存入一个临时数组。
3. 遍历完当前层后，将下一层的节点加入队列，重复上述操作。

代码实现：

#include <queue>
#include <vector>
using namespace std;

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        if (root == nullptr) return result;

        queue<TreeNode*> q;
        q.push(root);

        while (!q.empty()) {
            int levelSize = q.size(); // 当前层的节点数量
            vector<int> currentLevel;

            for (int i = 0; i < levelSize; ++i) {
                TreeNode* node = q.front();
                q.pop();
                currentLevel.push_back(node->val);

                // 将下一层的节点加入队列
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }

            result.push_back(currentLevel); // 将当前层加入结果
        }

        return result;
    }
};

---

方法 2：递归实现

通过递归实现层序遍历，记录每层的节点值。

核心逻辑：

1. 使用一个辅助函数 traverse，将每层的节点值存入结果数组。
2. 如果当前层不存在结果数组，先创建该层的数组。
3. 递归遍历左右子树，层数加 1。

代码实现：

#include <vector>
using namespace std;

class Solution {
public:
    void traverse(TreeNode* root, int level, vector<vector<int>>& result) {
        if (root == nullptr) return;

        // 如果当前层不存在，创建新的层
        if (result.size() <= level) {
            result.push_back({});
        }

        // 将当前节点值加入当前层
        result[level].push_back(root->val);

        // 递归处理左右子树
        traverse(root->left, level + 1, result);
        traverse(root->right, level + 1, result);
    }

    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        traverse(root, 0, result);
        return result;
    }
};

---

代码分析

方法 1：迭代

1. 时间复杂度: $O(n)$，每个节点访问一次。
2. 空间复杂度: $O(w)$，其中 $w$ 是树的最大宽度，队列中的最大节点数。

方法 2：递归

1. 时间复杂度: $O(n)$，每个节点访问一次。
2. 空间复杂度: $O(h)$，其中 $h$ 是树的高度，递归调用栈的深度。

---

示例运行

示例 1

输入：

root = [3,9,20,null,null,15,7]

输出：

[[3], [9,20], [15,7]]

示例 2

输入：

root = [1]

输出：

[[1]]

示例 3

输入：

root = []

输出：

[]

---

两种方法均可以正确实现层序遍历，选择迭代或递归视个人喜好及具体需求而定。

108. 将有序数组转换为二叉搜索树

问题描述

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。

示例 1：

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

• $1 <= nums.length <= 10^4$
• $-10^4 <= nums[i] <= 10^4$
• nums 按 严格递增 顺序排列

题解

以下是 LeetCode 108. 将有序数组转换为二叉搜索树 的 C++ 解法，利用递归构建平衡二叉搜索树。

---

方法：递归实现

通过递归的方式构建平衡二叉搜索树：

1. 每次选择数组的中间元素作为当前子树的根节点。
2. 左半部分数组递归构建左子树。
3. 右半部分数组递归构建右子树。

代码实现

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return buildTree(nums, 0, nums.size() - 1);
    }

private:
    TreeNode* buildTree(const vector<int>& nums, int left, int right) {
        if (left > right) return nullptr; // 递归终止条件

        int mid = left + (right - left) / 2; // 选择中间元素
        TreeNode* root = new TreeNode(nums[mid]); // 创建当前根节点

        // 构建左子树
        root->left = buildTree(nums, left, mid - 1);

        // 构建右子树
        root->right = buildTree(nums, mid + 1, right);

        return root;
    }
};

---

代码分析

时间复杂度

1. 构建树的时间复杂度: $O(n)$，每个节点访问一次。
2. 每层递归处理的元素是数组的一部分，总共递归处理的时间是线性的。

空间复杂度

1. 空间复杂度: $O(\log n)$，递归调用栈的深度等于树的高度，树的高度为 $\log n$（平衡树）。

---

示例运行

示例 1

输入：

nums = [-10, -3, 0, 5, 9]

输出：

[0, -3, 9, -10, null, 5]

解释：

• 根节点为 0。
• 左子树由数组 [−10,−3][-10, -3] 构建。
• 右子树由数组 [5,9][5, 9] 构建。

---

示例 2

输入：

nums = [1, 3]

输出：

[3, 1]

解释：

• 根节点为 3。
• 左子树由数组 [1][1] 构建。
• 或根节点为 1，右子树由数组 [3][3] 构建。

---

优化与提示

• 选择数组中间元素作为根节点可以保证树的平衡性。
• 如果允许自定义构造规则，也可以选择中间靠左或靠右的元素，效果相同。

98. 验证二叉搜索树

问题描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在$[1, 10^4]$ 内
• $-2^31 <= Node.val <= 2^31 - 1$

题解

以下是 LeetCode 98. 验证二叉搜索树 的 C++ 解法，提供递归和迭代两种实现方式。

---

方法 1：递归实现（上下界限制）

核心思路：

• 使用上下界限制每个节点的合法值范围：
  • 左子树的所有节点值必须小于当前节点值。
  • 右子树的所有节点值必须大于当前节点值。
• 递归时将上下界传递到子树，动态更新其合法范围。

代码实现：

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        return validate(root, nullptr, nullptr);
    }

private:
    bool validate(TreeNode* node, TreeNode* minNode, TreeNode* maxNode) {
        if (node == nullptr) return true; // 空树合法

        // 当前节点值必须在 (minNode->val, maxNode->val) 范围内
        if ((minNode && node->val <= minNode->val) || 
            (maxNode && node->val >= maxNode->val)) {
            return false;
        }

        // 递归检查左子树和右子树
        return validate(node->left, minNode, node) && 
               validate(node->right, node, maxNode);
    }
};

---

方法 2：迭代实现（中序遍历）

核心思路：

• 二叉搜索树的中序遍历结果是一个严格递增的序列。
• 使用栈进行中序遍历，记录前一个节点值，确保当前节点值总是大于前一个节点值。

代码实现：

#include <stack>
using namespace std;

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> s;
        TreeNode* prev = nullptr;

        while (!s.empty() || root) {
            // 左子树全部入栈
            while (root) {
                s.push(root);
                root = root->left;
            }

            // 访问栈顶节点
            root = s.top();
            s.pop();

            // 检查中序遍历的顺序是否严格递增
            if (prev && root->val <= prev->val) {
                return false;
            }
            prev = root;

            // 处理右子树
            root = root->right;
        }

        return true;
    }
};

---

代码分析

方法 1：递归实现

1. 时间复杂度: $O(n)$，每个节点访问一次。
2. 空间复杂度: $O(h)$，其中 $h$ 是树的高度，递归调用栈的深度。

方法 2：迭代实现

1. 时间复杂度: $O(n)$，每个节点访问一次。
2. 空间复杂度: $O(h)$，其中 $h$ 是树的高度，栈的最大深度。

---

示例运行

示例 1

输入：

root = [2,1,3]

输出：

true

示例 2

输入：

root = [5,1,4,null,null,3,6]

输出：

false

---

方法选择

• 如果更熟悉递归，方法 1 是更直观的实现。
• 如果需要避免递归调用栈溢出，方法 2 使用显式栈管理更适合大规模数据。